参考:https://qiita.com/quzq/items/c1a4929f47d986b0f77f
回帰直線とは全データの中心的な分布傾向を示す直線で、全データの誤差の二乗が最小になるような線である。
これは最小二乗法によって求められる。
モデル関数を f(x) = ax + b という一次関数とすると、
aとbは次のように求められる。
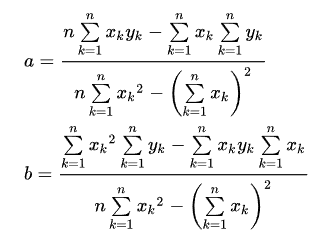
// 回帰直線を求める(最小二乗法)
const lsm = coordinates => {
const n = coordinates.length;
// Xの合計
const sigX = coordinates.reduce((acc, c) => acc + c.x, 0);
// Yの合計
const sigY = coordinates.reduce((acc, c) => acc + c.y, 0);
// Xの2乗の合計
const sigXX = coordinates.reduce((acc, c) => acc + c.x * c.x, 0);
// X×Yの2乗の合計
const sigXY = coordinates.reduce((acc, c) => acc + c.x * c.y, 0);
// a(傾き)を求める
const a = (n * sigXY - sigX * sigY) / (n * sigXX - Math.pow(sigX, 2));
// b(切片)を求める
const b = (sigXX * sigY - sigXY * sigX) / (n * sigXX - Math.pow(sigX, 2));
return { a, b };
}